Astar Search Algorithm
Astar Algorithm
In computer science, A* (pronounced “A star”) is a computer algorithm that is widely used in pathfinding and graph traversal, which is the process of finding a path between multiple points, called “nodes”. It enjoys widespread use due to its performance and accuracy. However, in practical travel-routing systems, it is generally outperformed by algorithms which can pre-process the graph to attain better performance,[1] although other work has found A* to be superior to other approaches.[2]
Peter Hart, Nils Nilsson and Bertram Raphael of Stanford Research Institute (now SRI International) first published the algorithm in 1968.[3] It can be seen as an extension of Edsger Dijkstra’s 1959 algorithm. A* achieves better performance by using heuristics to guide its search.
A* is an informed search algorithm, or a best-first search, meaning that it is formulated in terms of weighted graphs: starting from a specific starting node of a graph, it aims to find a path to the given goal node having the smallest cost (least distance travelled, shortest time, etc.). It does this by maintaining a tree of paths originating at the start node and extending those paths one edge at a time until its termination criterion is satisfied.
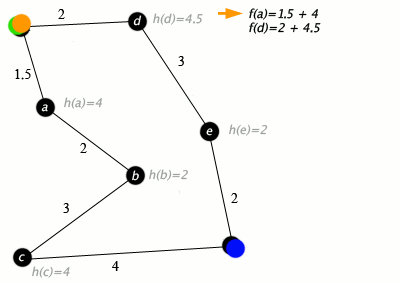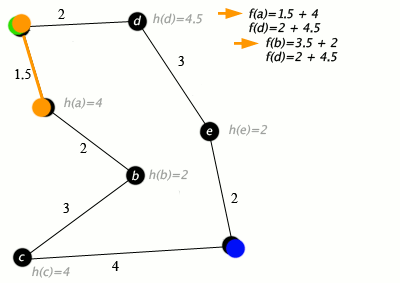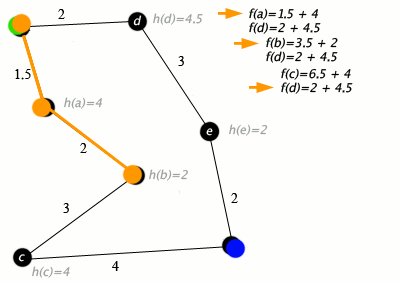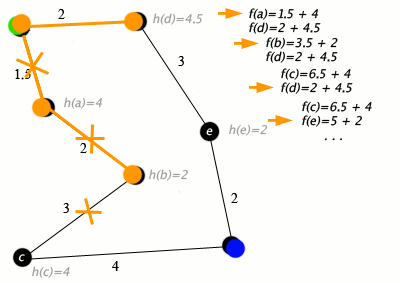
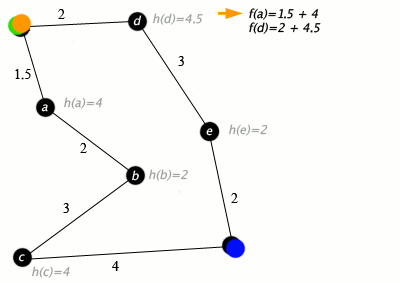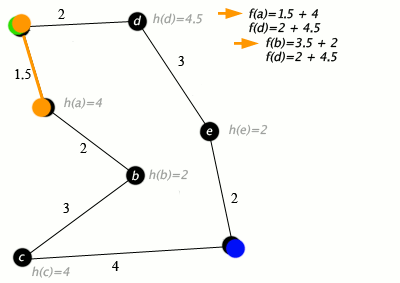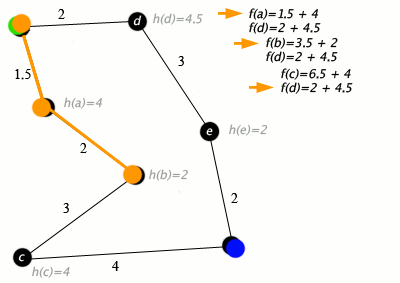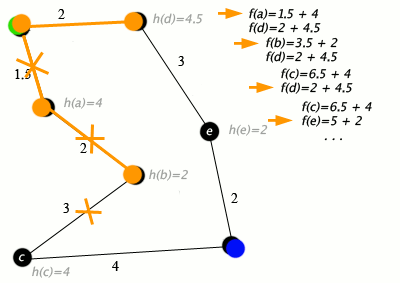
At each iteration of its main loop, A* needs to determine which of its paths to extend. It does so based on the cost of the path and an estimate of the cost required to extend the path all the way to the goal. Specifically, A* selects the path that minimizes
f(n)=g(n)+h(n)} f(n)=g(n)+h(n)
where n is the next node on the path, g(n) is the cost of the path from the start node to n, and h(n) is a heuristic function that estimates the cost of the cheapest path from n to the goal. A* terminates when the path it chooses to extend is a path from start to goal or if there are no paths eligible to be extended.The heuristic function is problem-specific. If the heuristic function is admissible, meaning that it never overestimates the actual cost to get to the goal, A* is guaranteed to return a least-cost path from start to goal.

References